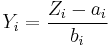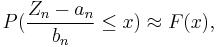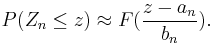Asymptotic distribution

In mathematics and statistics, an asymptotic distribution is a hypothetical distribution that is in a sense the "limiting" distribution of a sequence of distributions. One of the main uses of the idea of an asymptotic distribution is in providing approximations to the cumulative distribution functions of statistical estimators.

Contents

Definition

A sequence of distributions corresponds to a sequence of random variables Zi for i = 1, 2, ... In the simplest case, an asymptotic distribution exists if the probability distribution of Zi converges to a probability distribution (the asymptotic distribution) as i increases: see convergence in distribution. A special case of an asymptotic distribution is when the sequence of random variables always approaches zero—that is, the Zi go to 0 as i goes to infinity. Here the asymptotic distribution is a degenerate distribution, corresponding to the value zero.

However, the most usual sense in which the term asymptotic distribution is used arises where the random variables Zi are modified by two sequences of non-random values. Thus if

Y_i=\frac{Z_i-a_i}{b_i}

converges in distribution to a non-degenerate distribution for two sequences {ai} and {bi} then Zi is said to have that distribution as its asymptotic distribution. If the distribution function of the asymptotic distribution is F then, for large n, the following approximations hold

P(\frac{Z_n-a_n}{b_n} \le x) \approx F(x) ,
P(Z_n \le z) \approx F(\frac{z-a_n}{b_n}) .

If an asymptotic distribution exists, it is not necessarily true that any one outcome of the sequence of random variables is a convergent sequence of numbers. It is the sequence of probability distributions that converges.

Asymptotic normality

See also: local asymptotic normality

Perhaps the most common distribution to arise as an asymptotic distribution is the normal distribution. In particular, the central limit theorem provides an example where the asymptotic distribution is the normal distribution.

Barndorff-Nielson & Cox[1] provide a direct definition of asymptotic normality.

The Binomial distribution seems to be the first asymptotic approximation by a normal distribution; compared to the more general case of central limit theorem, convergence of the Binomial to the normal is especially rapid. Asymptotic normality of the Binomial distribution is proven by the de Moivre–Laplace theorem.

See also

References

  1. ^ Barndorff-Nielson, O.E., Cox, D.R. (1989) Asymptotic Techniques for Use in Statistics. Chapman and Hall. ISBN 0-412-31400-2